지니계수
소득의 불평등 정도를 나타내는 가장 대표적인 소득분배지표입니다. 지니계수는 0에서 1사이의 수치로 표시되는데 소득분배가 완전평등한 경우가 0, 완전불평등한 경우가 1입니다.

지니계수는 로렌츠곡선을 이용하여 계산할 수 있습니다. 로렌츠곡선을 그리기 위해서는 소득이 낮은 사람부터 높은 사람 순으로 전체 인구를 나열하여 총인구를 100으로 설정하고 가로축은 인구누적비율로, 세로축은 이 사람들의 소득을 차례로 누적한 총소득을 100으로 하는 소득누적비율로 설정합니다. 그리고 인구누적비율과 해당소득누적비율을 연결한 선을 로렌츠곡선이라고 정의합니다.
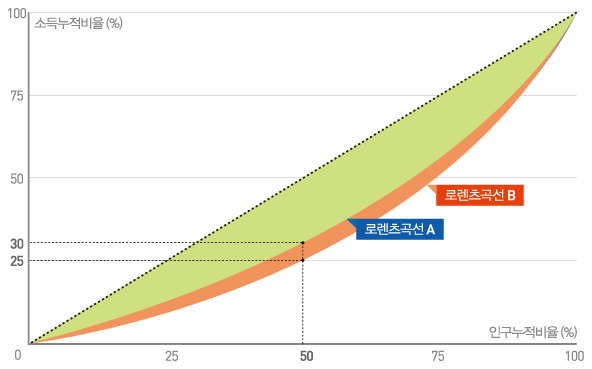
그림에서 보면 사각형에서 대각선은 인구누적비율과 소득누적비율이 일치하는, 즉 모든 인구가 동일한 소득을 보유해 완전히 평등한 소득분배를 보여줍니다. 그러나 현실에서는 완전히 평등한 소득분배가 이뤄지지 않기 때문에 곡선 A 또는 B와 같은 로렌츠곡선이 만들어집니다. 로렌츠곡선 A와 B를 비교했을 때 전체 인구의 50%가 곡선 A의 경우 전체 소득의 30%를 점유하고 있지만, 곡선 B의 경우 전체 소득의 25%를 점유하고 있으므로 A보다 B에서 소득의 불평등 정도가 심한 것을 알 수 있습니다. 즉 대각선에서 멀어질수록 소득분배의 불평등 정도가 심한 것을 나타냅니다.
소득분배가 완전히 평등하다면, 즉 모든 사람의 소득이 같다면 대각선과 로렌츠곡선 사이의 면적이 0이 되어 지니계수 역시 0이 됩니다. 반대로 소득분배가 완전히 불평등하다면 로렌츠곡선은 직각의 형태를 갖게 됩니다. 이때는 대각선과 로렌츠곡선 사이의 면적이 대각선 아래 삼각형 전체의 면적과 일치하여 지니계수는 1이 됩니다.
출처: 통계청
로렌츠 곡선
경제학에서 로렌츠 곡선은 하위 x%의 가구가 y%의 소득이 분배될 때의 확률 분포를 누적 분포 함수의 그래프로 나타낸 것이다. 로렌츠 곡선은 소득 분배 정도를 나타낼 때 주로 이용된다. 가구의 누적 백분율은 x축에, 소득의 비율은 y축에 표시한다. 로렌츠 곡선은 재산의 분포를 나타내는 데에도 사용될 수 있으며 사회적 불평등의 정도를 측정하는 척도로 사용한다. 로렌츠 곡선은 맥스 O. 로렌츠가 소득 분포를 나타내기 위해 개발하였다.

로렌츠 곡선 위에 있는 모든 점은 "하위 x%의 가구는 총 소득의 y%를 얻는다"로 표현할 수 있다. 절대적 평등의 상황에서는 x=y가 성립한다. 한편 한 사람이 모든 재산을 차지하는 절대적으로 불평등한 사회에서는 "x" < 100%일 때 y = 0%이고 x=100%일 때 y=100%으로 나타낼 수 있다.
로렌츠 곡선에서 어떤 사회의 소득 분포를 나타낸 곡선과 절대적 평등의 선 사이의 면적이 곧 지니 계수이다. 지니 계수가 클수록 소득 분포의 불평등이 크다.
- 로렌츠 곡선은 항상 (0,0)에서 시작해 (1,1)에서 끝난다.
- 로렌츠 곡선은 확률분포의 평균이 0이거나 무한일 경우에는 정의되지 않는다.
- 확률분포에 대한 로렌츠 곡선은 연속함수이다. 하지만 불연속함수를 나타내는 곡선은 확률분포곡선의 극한으로 나타난다. 그 예로 절대적 불평등의 선을 들 수 있다.
- 측정하여 얻어지는 변수가 음수를 취할 수 없을 때:
- 로렌츠 곡선은 절대적 평등의 선 위로 올라가거나 절대적 불평등의 선 아래로 내려갈 수 없다.
- 곡선은 증가함수이며
- 볼록함수이다.
- 변수가 음수를 취할 수 있으나 평균이 양수일 때 로렌츠 곡선은 절대적 불평등의 선 아래로 내려가는 아래로 볼록한 함수이다.
- 변수로 음수를 취하고 평균이 음수일 때 로렌츠 곡선은 절대적 평등의 선 위로 올라가는 위로 볼록한 함수이다.
출처: 위키백과
분위배율
균등화 개인소득을 오름차순(적은 금액에서 많은 금액 순서)으로 정리하여 이들을 순서에 따라 동일한 규모의 집단으로 묶었을 때 집단별 평균소득을 서로 비교한 값입니다.
5분위 배율과 10분위 배율을 가장 많이 사용합니다.

5분위 배율은 균등화 개인소득 순서에 따라 전체 인구를 5개 그룹으로 나누었을 때 소득이 높은 5분위에 해당하는 개인들의 평균소득과 소득이 낮은 1분위에 해당하는 개인들의 평균소득 사이의 비율로, 5분위 소득이 1분위 소득의 몇 배인지를 보여줍니다. 예를 들어 5분위 배율이 5.43이라면 5분위 소득이 1분위 소득보다 5.43배 많다는 것을 의미합니다.
10분위 배율은 마찬가지로 10분위에 해당하는 개인들의 평균소득과 1분위에 해당하는 개인들의 평균소득 사이의 비율입니다.
백분위율
균등화 개인소득을 오름차순(적은 금액에서 많은 금액순서)으로 정리하여 이들을 순서에 따라 동일한 규모로 나눈 후 나뉜 각 집단을 분위라 칭합니다. 그리고 각 분위의 상한값을 P○○로 표시합니다. 이때 P○○ 사이의 비율을 백분위율 지표라고 정의하는데, 예를 들어 백분위율 P90/P10은 9분위 상한값과 1분위 상한값의 비율입니다.

10분위 기준으로 4분위의 상한값은 P40으로 표시하고 5분위 기준 2분위도 P40으로 표시합니다. 백분위율로 소득불평등을 측정할 때 P50/P10 또는 P90/P50의 비율을 많이 사용하는데 P50은 전체의 중위소득을 의미합니다. 그러므로 P50/P10 또는 P90/P50은 중위소득과 1분위의 상한값 비율 또는 9분위의 상한값과 중위소득의 비율을 의미합니다.
중위소득계층
소득만을 고려하여 중위소득의 50%초과 150% 이하에 해당하는 사람들이 중위소득계층에 해당합니다.

중위소득계층에 대한 통계는 전체 인구에서 중위소득계층에 해당하는 인구의 비율로 작성합니다. 그래프를 보면 인구누적비율 50%에 해당하는 소득, 즉 중위소득이 1,833천 원임을 알 수 있습니다. 중위소득의 50%에 해당하는 소득 917천 원과 중위소득의 150%에 해당하는 소득 2,750천 원에 해당하는 인구누적비율은 14.6%와 80.2%입니다. 따라서 중위소득계층에 해당하는 인구비율은 65.6%가 됩니다.
중위소득계층의 인구비율 통계는 하위소득계층이나 상위소득계층의 인구비율과 함께 최근 사람들의 소득계층 이동을 분석하는 데 이용됩니다. 즉 중위소득계층의 인구비율이 증가한 경우 이것이 하위소득계층에 속했던 사람들이 이로부터 벗어났기 때문인지 아니면 상위소득계층에 속했던 사람들의 소득이 줄었기 때문인지를 파악하는 것은 소득분배 정책의 중요한 지표가 됩니다.
참고 : 중위소득계층 가구의 소득

출처 : 통계청